The relationship between the differential scattering cross section
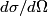 , the solid angle , the solid angle 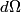 , the number of incident particles per unit time , the number of incident particles per unit time 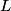 , the number of incident particles scattered into the solid angle , the number of incident particles scattered into the solid angle 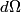 per unit time per unit time 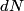 , and number of nuclei per unit area , and number of nuclei per unit area 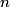 is %(see Griffiths QM page 399 but note that the notation there is slightly different) is %(see Griffiths QM page 399 but note that the notation there is slightly different)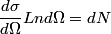 We are given that 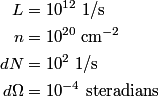 Plugging these values in, we find that 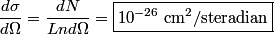 Therefore, answer (C) is correct. |